Practical Tips for Finetuning LLMs Using LoRA (Low-Rank Adaptation)

Things I Learned From Hundreds of Experiments

Low-rank adaptation (LoRA) is among the most widely used and effective techniques for efficiently training custom LLMs. For those interested in open-source LLMs, it's an essential technique worth familiarizing oneself with.

Last month, I shared an article with several LoRA experiments, based on the open-source Lit-GPT repository that I co-maintain with my colleagues at Lightning AI. This Ahead of AI article aims to discuss the primary lessons I derived from my experiments. Additionally, I'll address some of the frequently asked questions related to the topic.  If you are interested in finetuning custom LLMs, I hope these insights will save you some time in "the long run" (no pun intended).

In brief, the main takeaways I am discussing in this article are the following:

1. Despite the inherent randomness of LLM training (or when training models on GPUs in general), the outcomes remain remarkably consistent across multiple runs.

2. QLoRA presents a trade-off that might be worthwhile if you're constrained by GPU memory. It offers 33% memory savings at the cost of a 39% increase in runtime.

3. When finetuning LLMs, the choice of optimizer shouldn't be a major concern. While SGD on its own is suboptimal, there's minimal variation in outcomes whether you employ AdamW, SGD with a scheduler, or AdamW with a scheduler.

4. While Adam is often labeled a memory-intensive optimizer due to its introduction of two new parameters for every model parameter, this doesn't significantly affect the peak memory demands of the LLM. This is because the majority of the memory is allocated for large matrix multiplications rather than retaining extra parameters.

5. For static datasets, iterating multiple times, as done in multi-epoch training, might not be beneficial. It often deteriorates the results, probably due to overfitting.

6. If you're incorporating LoRA, ensure it's applied across all layers, not just to the Key and Value matrices, to maximize model performance.

7. Adjusting the LoRA rank is essential, and so is selecting an apt alpha value. A good heuristic is setting alpha at twice the rank's value.

8. 7 billion parameter models can be finetuned efficiently within a few hours on a single GPU possessing 14 GB of RAM. With a static dataset, optimizing an LLM to excel across all benchmark tasks is unattainable. Addressing this requires diverse data sources, or perhaps LoRA might not be the ideal tool.

In addition, I will answer ten common questions around LoRA:

• Q1: How Important is the Dataset?

• Q2: Does LoRA Work for Domain Adaptation?

• Q3: How Do You Select the Best Rank?

• Q4: Does LoRA Need to Be Enabled for All Layers?

• Q5: How To Avoid Overfitting?

• Q6: What about Other Optimizers?

• Q7: What Other Factors Influence Memory Usage?

• Q8: How Does it Compare to Full Finetuning and RLHF?

• Q9: Can LoRA Weights be Combined?

• Q10: What about Layer-wise Optimal Rank Adaptation?

(In the previous issue of AI, I mentioned that I wanted to write a more general introduction with a from-scratch code implementation of LoRA sometime if there's interest. According to your feedback, there's a lot of interest, and I plan to share another article on LoRA in the future. For now, this article is focused on the broader ideas and takeaways from working with LoRA—a top-down view.)

A Brief Introduction to LoRA

Large language models are large, and it can be expensive to update all model weights during training due to GPU memory limitations. 

For example, suppose we have an LLM with 7B parameters represented in a weight matrix W. (In reality, the model parameters are, of course, distributed across different matrices in many layers, but for simplicity, we refer to a single weight matrix here). During backpropagation, we learn a ΔW matrix, which contains information on how much we want to update the original weights to minimize the loss function during training.

The weight update is then as follows:

W_updated = W + ΔW

If the weight matrix W contains 7B parameters, then the weight update matrix ΔW also contains 7B parameters, and computing the matrix ΔW can be very compute and memory intensive.

The LoRA method proposed by Hu et al. replaces to decompose the weight changes, ΔW, into a lower-rank representation. To be precise, it does not require to explicitly compute ΔW. Instead, LoRA learns the decomposed representation of ΔW directly during training which is where the savings are coming from, as shown in the figure below.

As illustrated above, the decomposition of ΔW means that we represent the large matrix ΔW with two smaller LoRA matrices, A and B. If A has the same number of rows as ΔW and B has the same number of columns as ΔW, we can write the decomposition as ΔW = AB. (AB is the matrix multiplication result between matrices A and B.) 

How much memory does this save? It depends on the rank r, which is a hyperparameter. For example, if ΔW has 10,000 rows and 20,000 columns, it stores 200,000,000 parameters. If we choose A and B with r=8, then A has 10,000 rows and 8 columns, and B has 8 rows and 20,000 columns, that's 10,000×8 + 8×20,000 = 240,000 parameters, which is about 830× less than 200,000,000.

Of course, A and B can't capture all the information that ΔW could capture, but this is by design. When using LoRA, we hypothesize that the model requires W to be a large matrix with full rank to capture all the knowledge in the pretraining dataset. However, when we finetune an LLM, we don't need to update all the weights and capture the core information for the adaptation in a smaller number of weights than ΔW would; hence, we have the low-rank updates via AB.

1. LoRA Consistency

Running multiple experiments with LoRA, I found that the benchmark results are surprisingly consistent across the different runs despite the inherent randomness of LLM training or when training models on GPUs in general. This is a good basis for additional comparison studies.

(Note that the results were obtained with default settings using a small r=8. The experimental details can be found in my other article here.)

2. QLoRA Compute-Memory Trade-offs

QLoRA by Dettmers et al., short for quantized LoRA, is a technique that further reduces memory usage during finetuning. During backpropagation, QLoRA quantizes the pretrained weights to 4-bit precision and uses paged optimizers to handle memory spikes.

Indeed, I found that one can save 33% of GPU memory when using QLoRA. However, this comes at a 39% increased training runtime caused by the additional quantization and dequantization of the pretrained model weights in QLoRA.

Default LoRA with 16-bit brain floating point precision:

• Training time: 1.85 h

• Memory used: 21.33 GB

QLoRA with 4-bit Normal Floats:

• Training time: 2.79 h

• Memory used: 14.18 GB

Moreover, I found that the modeling performance was barely affected, which makes QLoRA a feasible alternative to regular LoRA training to work around the common GPU memory bottleneck.

3. Learning Rate Schedulers

Learning rate schedulers lower the learning rate throughout the training to optimize convergence and avoid overshooting the loss minima. 

Cosine annealing is a learning rate scheduler that adjusts the learning rate following a cosine curve. It starts with a high learning rate, which then decreases smoothly, approaching zero in a cosine-like manner. A commonly used variant is the half-cycle variant, where only a half-cosine cycle is completed over the course of training, as shown in the figure below.

As part of my experiments, I added a cosine annealing scheduler to the LoRA finetuning scripts and observed that it improved the SGD performance noticeably. However, it has less impact on Adam and AdamW optimizers and makes almost no difference.

The potential advantages of SGD over Adam are discussed in the next section.

4. Adam vs SGD

Adam and AdamW optimizers remain popular choices in deep learning even though they are very memory-intensive when we are working with large models. The reason is that Adam optimizers maintain two moving averages for each model parameter: the first moment (mean) of the gradients and the second moment (uncentered variance) of the gradients. In other words, Adam optimizers store two additional values for each single model parameter in memory. If we are working with a 7B parameter model, that's an extra 14B parameters to track during training.

SGD optimizers don't need to track any additional parameters during training, so a question is: what advantage does swapping Adam by SGD have on the peak memory requirements when training LLMs? 

In my experiments, training a 7B parameter Llama 2 model trained with AdamW and LoRA defaults (r=8) required 14.18 GB of GPU memory. Training the same model with SGD instead required 14.15 GB of GPU memory. In other words, the savings (0.03 GB) were minimal. 

Why are the memory savings so small? That's because with LoRA, we only have a small number of trainable parameters. For instance, if r=8, we have 4,194,304 trainable LoRA parameters out of all 6,738,415,616 parameters in a 7B Llama 2 model. 

If we just look at the bare numbers, 4,194,304 trainable parameters still sound like a lot, but if we do the math, we only have 4,194,304 × 2 × 16 bit = 134.22 megabits = 16.78 megabytes. (We observed a 0.03 Gb = 30 Mb difference since there is an additional overhead in storing and copying optimizer states.) The 2 represents the number of extra parameters that Adam stores, and the 16-bit refers to the default precision for the model weights.

However, if we increase the LoRA r to 256, something I've done in later experiments, the difference between Adam and SGD optimizers becomes more noticeable:

• 17.86 GB with AdamW

• 14.46 GB with SGD

As a takeaway, swapping Adam optimizers with SGD may not be worthwhile when LoRA's r is small. However, it may be worthwhile when we are increasing r. 

5. Multiple Training Epochs

In conventional deep learning, we often iterate over a training set multiple times -- an iteration over the training set is called an epoch. It's common to run hundreds of training epochs when training convolutional neural networks, for example. Is multi-epoch training useful for instruction finetuning as well?

When I increased the number of iterations for the 50k-example Alpaca instruction finetuning dataset by a factor of two (analogous to 2 training epochs), I noticed a decline in model performance.

The takeaway is that multi-epoch training might not benefit instruction finetuning since it can deteriorate the results. I observed the same with the 1k-example LIMA dataset. This performance decline is likely due to increased overfitting, which warrants additional investigation.

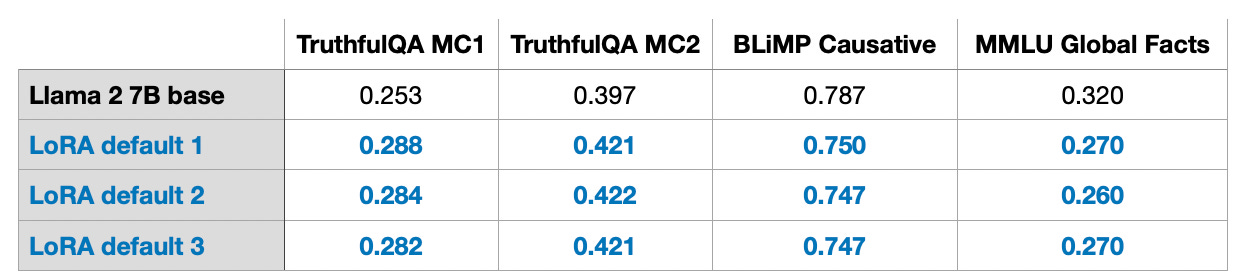
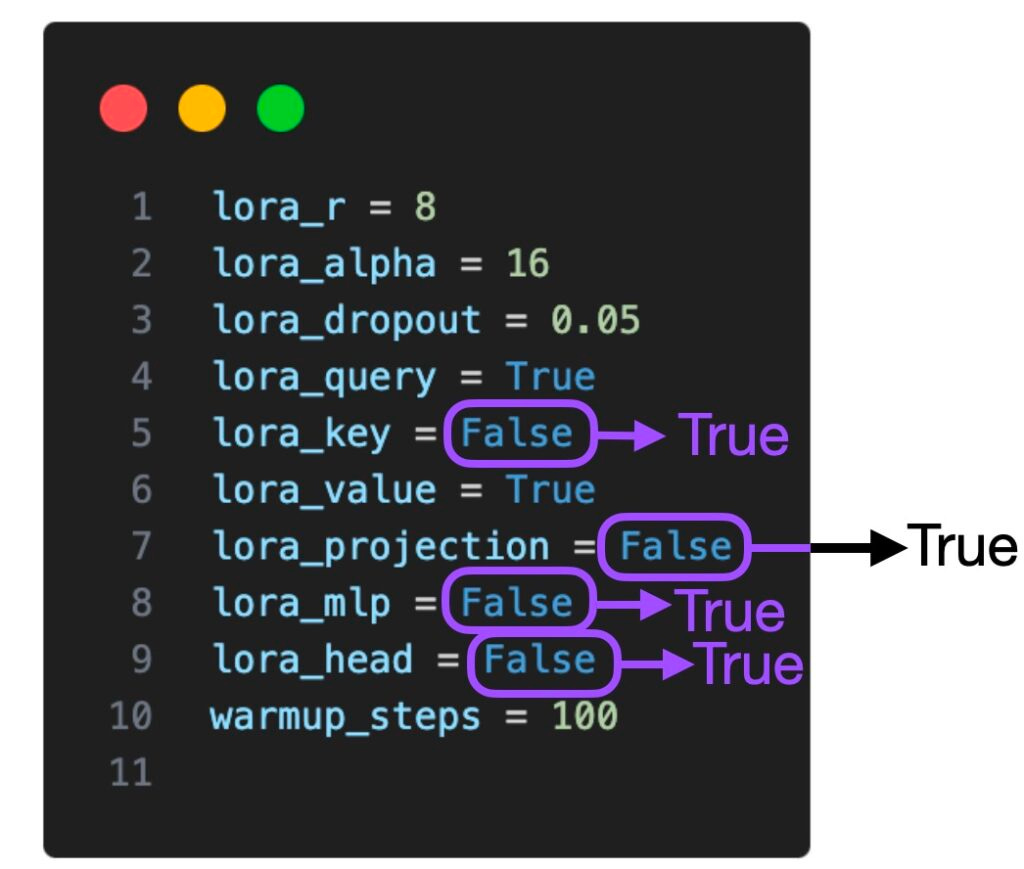
6. Enable LoRA for More Layers

The tables above showed experiments where LoRA was only enabled for select weight matrices, i.e., the Key and Value weight matrices in each transformer layer. In addition, we can also enable LoRA for the Query weight matrices, the projection layers, the other linear layers between the multihead attention blocks, and the linear output layer. 

If we enable LoRA for all these additional layers, we increase the number of trainable parameters by a factor of 5, from 4,194,304 to 20,277,248, for a 7B Llama 2 model. This also comes with a larger memory requirement (16.62 GB instead of 14.18 GB) but can increase the modeling performance noticeably.

However, a limitation of my experiment is that I only explored two settings: (1) LoRA for only the query and value weight matrices enabled, and (2) LoRA for all layers enabled. It might be worthwhile exploring the other combinations in future experiments. For example, it would be interesting to know whether activating LoRA for the projection layer is actually beneficial.

7. Balancing LoRA Hyperparameters: R and Alpha

As the original LoRA paper outlines, LoRA introduces an additional scaling coefficient for applying the LoRA weights to the pretrained weights during the forward pass. The scaling involves the rank parameter r, which we discussed earlier, as well as another hyperparameter α (alpha) that is applied as follows:

scaling = alpha / r
weight += (lora_B @ lora_A) * scaling 

As we can see in the code formula above, the larger the influence of the LoRA weights.

Previous experiments used r=8 and alpha=16, which resulted in a 2-fold scaling. Choosing alpha as two times r is a common rule of thumb when using LoRA for LLMs, but I was curious if this still holds for larger r values. In other words, “alpha = 2×rank” really seems to be a sweet spot. However, in this specific combination of model and dataset, where r=256 and alpha=128 (a 0.5-fold scaling) performance is even better.

(I experimented with r=32, r=64, r=128, and r=512 but omitted the results for clarity as r=256 resulted in the best performance.)

Choosing alpha as two times as large as r may often result in the best outcomes, but it may also not hurt to experiment with different ratios.

8. Training 7B Parameter Models on a Single GPU

One of the main takeaways is that LoRA allows us to finetune 7B parameter LLMs on a single GPU. In this particular case, using QLoRA with the best setting (r=256 and alpha=512) requires 17.86 GB with AdamW and takes about 3 hours (on an A100) for 50k training examples (here, the Alpaca dataset).

In the remaining sections of this article, I am answering additional questions you might have.

Answers to Common Questions

Q1: How Important is the Dataset?

The dataset can be critical. I used the Alpaca dataset, which contains 50k training examples, for my experiments. I chose this dataset because it's quite popular, and experimenting with different datasets was out of scope due to the already extensive length of the article.

However, it's worth noting that Alpaca is a synthetic dataset that was generated by querying an old version of ChatGPT and is probably not the best by today's standards. 

Data quality can be very important. For example, in June, I discussed the LIMA dataset (Ahead of AI #9: LLM Tuning & Dataset Perspectives), a curated dataset consisting of only 1k examples.

According to the LIMA: Less Is More for Alignment paper, a 65B Llama model finetuned on LIMA noticeably outperforms a 65B Llama model finetuned on Alpaca.

Using the best configuration (r=256, alpha=512) on LIMA, I got similar, if not better, performance than the 50x larger Alpaca dataset.

Q2: Does LoRA Work for Domain Adaptation?

Unfortunately, I don't have a good answer to this question. As a rule of thumb, knowledge is usually absorbed from the pretraining dataset. Instruction finetuning is generally more about helping or guiding the LLM towards following instructions. 

However, it's worth noting that if memory is a concern, LoRA can also be used for further pretraining existing pretrained LLMs on domain-specific datasets. 

Note that my experiments also included two arithmetic benchmarks (they are included in my other more technical write-up), on which LoRA-finetuned models performed significantly worse than the pretrained base models. My hypothesis is that the model unlearned arithmetic because the Alpaca dataset did not contain corresponding examples. Whether the model completely lost the knowledge or whether it's because the model can't handle the instructions anymore would require further investigation. However, a takeaway here is that it's probably a good idea to include examples of each task you care about when finetuning LLMs.

Q3: How Do You Select the Best Rank?

Unfortunately, I don't have any good heuristic for selecting a good r and think that it's a hyperparameter that needs to be explored for each LLM and each dataset. I suspect that choosing an r that is too large could result in more overfitting. On the other hand, a small r may not be able to capture diverse tasks in a dataset. In other words, I suspect that the more diverse the tasks in the dataset, the larger the r should be. For example, if I only want a model that carries out basic 2-digit arithmetic, then a tiny r might already be sufficient. However, this is only a hypothesis and would require additional investigation.

Q4: Does LoRA Need to Be Enabled for All Layers?

I only explored two settings: (1) LoRA for only the query and value weight matrices enabled, and (2) LoRA for all layers enabled. It might be worthwhile exploring the other combinations in future experiments. For example, it would be interesting to know whether activating LoRA for the projection layer is actually beneficial.

For instance, if we consider the various settings (lora_query, lora_key, lora_value, lora_projection, lora_mlp, and lora_head), that's 2^6 = 64 combinations to explore. This exploration would be an interesting topic for future studies.

Q5: How To Avoid Overfitting?

Generally, a larger r can lead to more overfitting because it determines the number of trainable parameters. If a model suffers from overfitting, decreasing r or increasing the dataset size are the first candidates to explore. Moreover, you could try to increase the weight decay rate in AdamW or SGD optimizers, and you can consider increasing the dropout value for LoRA layers. 

The LoRA dropout parameter that I haven't explored in my experiments (I used a fixed dropout rate of 0.05), is an interesting topic for future investigations.

Q6: What about Other Optimizers?

Other interesting optimizers for LLMs are worth exploring in the future. One such optimizer is Sophia: A Scalable Stochastic Second-order Optimizer for Language Model Pre-training, which was published in May.

Sophia is a second-order optimization algorithm that promises to be particularly attractive for LLMs where Adam and AdamW are usually the dominant ones. Compared to Adam, Sophia is 2× faster, and models trained with Sophia can achieve better modeling performance, according to the paper. In a nutshell, Sophia normalizes the gradients by gradient curvature instead of gradient variance, as in Adam.

Q7: What Other Factors Influence Memory Usage?

Besides precision and quantization settings, the model size, the batch size, and the number of trainable LoRA parameters, the dataset can also influence memory usage.

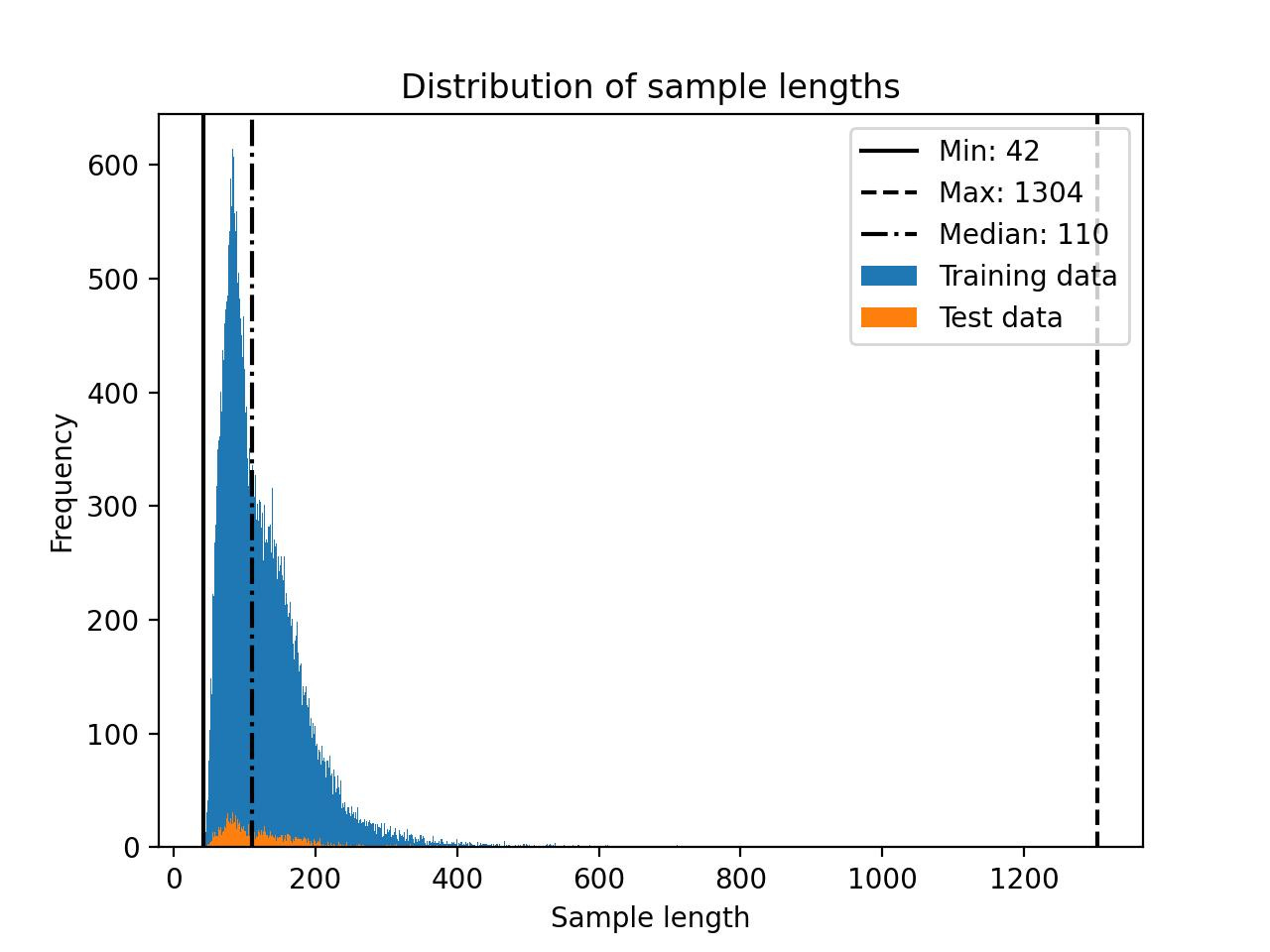
Note that Llama 2 has a block size of 4048. For instance, if an LLM has a block size of 4048 tokens, it can process sequences of up to 4048 tokens at once. However, shorter training sequences can result in substantial memory savings due to the masking of future tokens.

For example, the Alpaca dataset is relatively small, with a maximum length of 1304 tokens.

When I experimented with other datasets that had lengths of up to 2048 tokens, I noticed that the memory usage went up from 17.86 GB to 26.96 GB. 

Q8: How Does it Compare to Full Finetuning and RLHF?

I did not run any RLHF experiments (for those who are curious, I covered RLHF here), but I did consider full finetuning. Full finetuning required at least 2 GPUs and was completed in 3.5 h using 36.66 GB on each GPU. However, the benchmark results were not very good, likely due to overfitting or suboptimal hyperparameters.

Q9: Can LoRA Weights be Combined?

Yes, it's possible to combine multiple sets of LoRA weights. During training, we keep the LoRA weights separate from the pretrained weights and add them during each forward pass. 

However, If you have a real-world application with many sets of LoRA weights, for example, one set for each application customer, it makes sense to store these weights separately to save disk space. However, it's possible to merge the pretrained weights with the LoRA weights after training to create a single model. This way, we don't have to apply the LoRA weights in each forward pass:

weight += (lora_B @ lora_A) * scaling

Instead, we apply the weight update as shown above and save the merged (added) weights.

Similarly, we can keep adding multiple LoRA weight sets:

weight += (lora_B_set1 @ lora_A_set1) * scaling_set1
weight += (lora_B_set2 @ lora_A_set2) * scaling_set2
weight += (lora_B_set3 @ lora_A_set3) * scaling_set3
...

I have yet to do experiments to evaluate the performance of such an approach, but this is technically already possible via the scripts/merge_lora.py script provided in Lit-GPT.

Q10: What about Layer-wise Optimal Rank Adaptation?

For simplicity, we usually train deep neural networks with the same learning rate for each layer, and the learning rate is a hyperparameter that we need to optimize. To take it further, we can also choose a different learning rate for each layer (in PyTorch, this is not too complicated). However, it's rarely done in practice because it adds additional overhead, and there are usually already so many knobs to tune when training deep neural networks.

Analogous to choosing different learning rates for different layers, we can also choose different LoRA ranks for different layers. I haven't found any experiments on this, but a document that details this approach is Layer-wise Optimal Rank Adaptation (also abbreviated LORA). In theory, this sounds like a good idea in practice. However, it also adds an extensive number of choices when optimizing hyperparameters.

---

This magazine is a personal passion project. For those who wish to support me, please consider purchasing a copy of my Build a Large Language Model (From Scratch) book. (I am confident that you'll get lots out of this book as it explains how LLMs work in a level of detail that is not found anywhere else.)

Build a Large Language Model (From Scratch) now available on Amazon

If you read the book and have a few minutes to spare, I'd really appreciate a brief review. It helps us authors a lot!

Alternatively, I also recently enabled the paid subscription option on Substack to support this magazine directly.